
Yuk, kenali istilah-istilah statistik data tunggal dalam matematika! Ada mean, median, modus, jangkauan, kuartil, simpangan rata-rata, dan lain sebagainya.
—
Siapa yang suka dengan proses pengolahan data dan angka-angka? Atau ada yang sudah pernah melakukan proses pengolahan data sebelumnya? Nah, proses pengolahan data ini erat sekali kaitannya dengan
statistika
, lho! Kamu tentu sudah familiar dengan istilah statistika, kan?
Dalam statistika, ada berbagai istilah nih, teman-teman. Di antaranya terdapat istilah-istilah statistik data tunggal.
Data tunggal itu yang kayak gimana, sih? Data tunggal itu adalah
data yang disusun sendiri menurut nilai dan besarnya masing masing
. Kayak gini nih, contohnya:
5, 4, 7, 4, 6, 3, 7, 8
Nah, pada statistik data tunggal, a
da 9 istilah yang harus kalian pahami. Kesembilan istilah tersebut adalah
mean (rataan hitung)
,
modus
,
median
,
jangkauan
,
kuartil
,
simpangan kuartil
,
simpangan rata-rata
,
ragam
, dan
simpangan baku
.
Wah, banyak juga ya…
Eits
, tapi tenang! Pembahasan di artikel ini nggak akan bikin kamu pusing kaya gambar
header
di atas, kok. Kalau nggak percaya, yuk baca sampai selesai!
Mean (Rata-Rata)
Teman-teman, mean atau disebut juga sebagai rata-rata atau rataan hitung merupakan
rata-rata nilai hasil hitung
.
Maksudnya adalah nilai rata-rata yang muncul apabila seluruh data dijumlahkan dan dibagi sama rata sesuai jumlah data yang ada.
Contohnya yaitu
nilai rata-rata ulangan matematikamu selama semester 1 di kelas XII
.
Hayoo
, nilai rata-ratanya bagus nggak, nih? Atau ada yang justru masih penasaran gimana cara menghitungnya? Buat yang masih belum tau, nih, ada rumus yang bisa kamu pakai untuk menghitung mean atau rata-rata. Lihat rumusnya di bawah, ya!

Berdasarkan rumus di atas, mean bisa dihitung dengan cara
menjumlahkan semua data, lalu hasilnya dibagi dengan banyaknya data yang ada
. Misalnya kamu memiliki 5 data yang terdiri atas angka-angka sebagai berikut:
6, 9, 3, 5, 2
Maka,
mean atau rata-ratanya
adalah:
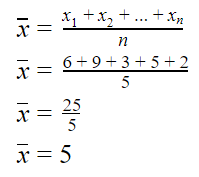
Jadi,
mean
atau rata-ratanya
adalah 5
. Mudah, kan? Sekarang, kita lanjut ke modus, yuk!
Modus
Modus yang dimaksud di sini bukan modus kriminal atau modus ke gebetan ya, teman-teman! Modus dalam statistika adalah
data yang paling sering muncul
atau
data yang memiliki frekuensi terbesar
di antara data-data lainnya.
Nah, sekarang coba kamu tebak, ya. Kalau di antara data tunggal berikut:
6, 6, 6, 7, 8, 9, 9, 9, 9, 9, 5
Modusnya yang mana,
hayoo
?
Yup, betul!
Modusnya adalah
9
, karena 9 merupakan data yang paling sering muncul, dengan frekuensi sebesar 5. Biasanya, siswa paling suka ngerjain contoh soal modus nih, soalnya nggak perlu pake rumus yang ribet
hehehe
..
Median
Kamu sudah tau apa artinya median? Median itu adalah
nilai tengah
. Kamu tahu nggak, sih, untuk menentukan median, ada
2 kasus yang harus diperhatikan
. Kasus pertama adalah
median untuk
data ganjil
dan kasus kedua adalah
untuk
data genap
. Kenapa dibagi 2 kasus? Karena rumus yang dipakai untuk menghitungnya itu berbeda ya,
guys
!
Hmm
.. seperti apa sih, rumusnya? Coba perhatikan gambar berikut, ya!

Hati-hati, jangan sampai tertukar antara rumus median untuk data ganjil dengan rumus median untuk data genap, ya! Teliti lagi supaya hasil pengolahan data statistikamu tidak salah.
Untuk median, contoh soalnya adalah sebagai berikut:
Median dari data tunggal
7, 6, 5, 3, 4, 2, 7, 6, 7
adalah…
Sebelum menghitung median, kita harus
mengurutkan
terlebih dahulu data yang ada,
dari nilai terkecil hingga terbesar
. Jika diurutkan, maka data akan menjadi seperti berikut:
2, 3, 4, 5, 6, 6, 7, 7, 7
Lalu, karena n data tersebut adalah
ganjil
, yaitu 9, maka kita menggunakan
rumus median untuk n ganjil
, ya! Jadinya seperti berikut ini:
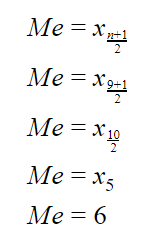
Jadi,
mediannya adalah data ke-5, yaitu 6
.
Hayoo
, jawabanmu betul, nggak?
Jangkauan (
Range
)
Sesuai dengan namanya,
jangkauan atau disebut juga
range
(rentang) adalah nilai data yang paling besar dan nilai data yang paling kecil
. Jangkauan digunakan untuk
menghitung selisih nilai tertinggi dan nilai terkecil
dalam kelompok data tersebut. Oleh karena itu, rumus yang digunakan untuk menghitung jangkauan adalah
R = x
max
– x
min
Contoh soal:
Hitunglah jangkauan dari data tunggal di bawah ini:
2, 3, 10, 8, 2, 3, 5, 6, 7, 3, 10, 8, 2, 3, 5, 6, 7
R = x
max
– x
min
R = 10 – 2
R = 8
Data terbesar (X
max
)
dari data tersebut adalah
10
, sedangkan
data terkecilnya (X
min
)
adalah
2
. Maka,
jangkauan
dari data tunggal tersebut
adalah 10 – 2 yaitu
8
.
Paham sampai sini? Yuk, lanjut lagi!
Baca juga:
Statistika Deskriptif dalam Data Berinterval
Kuartil
Kuartil atau Q
i
adalah nilai yang
membagi sekumpulan data yang telah diurutkan (dari terkecil hingga terbesar) ke dalam 4 bagian sama besar
. Wah, maksudnya apa ya? Ilustrasinya kurang lebih seperti ini nih, simak baik-baik ya!
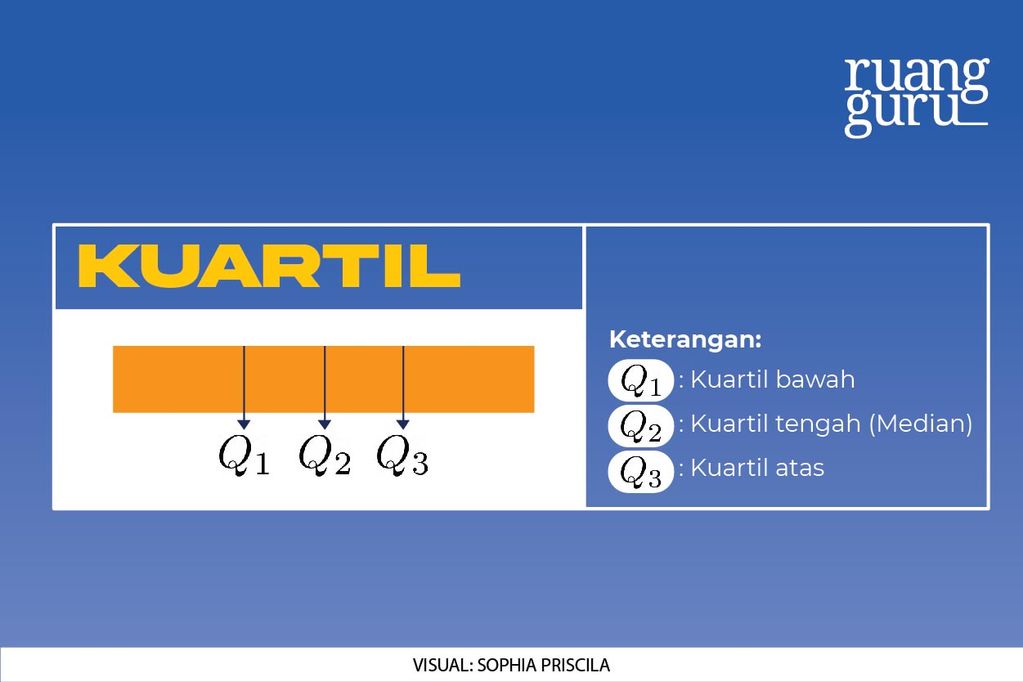
Ada tiga macam kuartil yaitu
kuartil bawah (Q
1
)
,
kuartil tengah
atau sama saja dengan
median (Q
2
)
, serta
kuartil atas (Q
3
)
. Untuk contohnya kamu bisa lihat setelah pembahasan simpangan kuartil berikut ini, ya!
Simpangan Kuartil
Ada kuartil, ada simpangan kuartil.
Hmm
.. kalau simpangan kuartil itu apa, ya? Nah, yang dimaksud dengan simpangan kuartil adalah
jangkauan dari ketiga kuartil itu sendiri
. Kamu bisa menghitung simpangan kuartil dengan rumus berikut:

Rumusnya yaitu setengah dari Q
3
dikurangi Q
1
. Wah, kalau rumusnya pendek gini, biasanya gampang mengingatnya, nih!
Contoh soal:
Hitunglah simpangan kuartil dari data berikut:
7, 10, 12, 14, 15, 17, 19, 20, 23, 25, 35
Tentukan terlebih dahulu Q
1
, Q
2
, dan Q
3
nya. Berdasarkan pengertiannya, kuartil membagi sekumpulan data yang telah diurutkan (dari terkecil hingga terbesar) ke dalam 4 bagian sama besar. Maka Q
1
, Q
2
, dan Q
3
nya adalah sebagai berikut:
7, 10,
12
, 14, 15,
17
, 19, 20,
23
, 25, 35
Maka, simpangan kuartilnya adalah sebagai berikut:
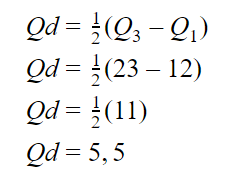
Q
3
dari data tersebut
adalah
23
dan
Q
1
nya
adalah
12
, maka
simpangan kuartil
dari data tunggal tersebut
adalah 5,5
.
Simpangan Rata-Rata
Selain simpangan kuartil, ada juga yang namanya simpangan rata-rata. Simpangan rata-rata adalah
rata-rata dari selisih data dengan nilai rata-rata datanya
. Bingung, ya? Coba perhatikan rumus simpangan rata-rata berikut ini deh, supaya kamu lebih ada gambaran.

Rumus simpangan rata-rata ini agak panjang, jadi pastikan kamu memperhatikan dengan baik, ya! Oh iya, hasil penghitungan dari simpangan rata-rata itu
selalu positif
. Jadi, kalau hasilnya negatif, kayaknya kamu salah menghitungnya deh.
Hehehe
..
Contoh soal:
Simpangan rata-rata data
9, 3, 7, 8, 4, 5, 4, 8
adalah…
Untuk menghitung simpangan rata-rata, kita perlu menghitung
rata-rata atau meannya
terlebih dahulu, yakni sebagai berikut:
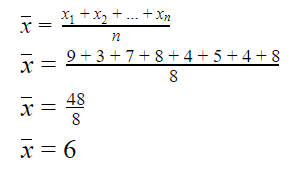
Setelah itu, kita gunakan rumus
simpangan rata-rata
, yakni sebagai berikut:
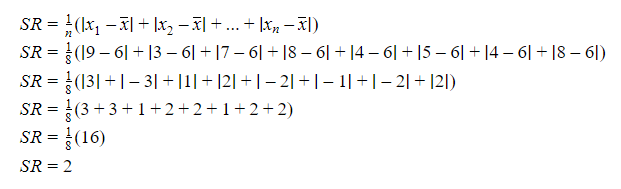
Jadi,
simpangan rata-rata
data tersebut
adalah 2
. Begitulah cara mencari simpangan rata-rata ya,
gengs
!
Ragam
Ragam yang dimaksud dalam statistik bukan ragam makanan favorit atau ragam acara televisi favorit, ya.
Hihihi
.. Ragam dalam statistika merupakan
rata-rata dari kuadrat selisih data dengan nilai rata-rata datanya
. Sama halnya dengan simpangan rata-rata,
rumus dari ragam juga agak panjang nih, jadi perhatikan baik-baik, ya!

Langsung kita coba kerjakan contoh soal, yuk! Misalnya kita memiliki data sebagai berikut:
6, 7, 8, 8, 10, 9
Sama halnya dengan simpangan rata-rata, kita perlu menghitung
meannya
terlebih dahulu, yakni sebagai berikut:
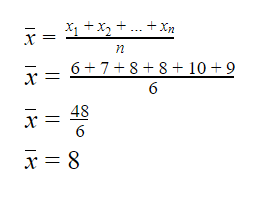
Maka,
ragam
dari data tersebut adalah:
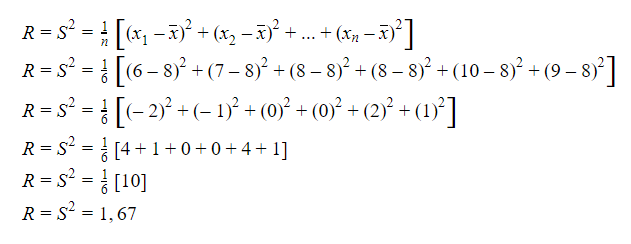
Jadi,
ragam dari data tersebut adalah
1,67
. Gimana? Sudah mulai pusing?
Eits
, jangan pusing duluu! Tinggal satu istilah lagi, nih!
Simpangan Baku
Istilah statistik data tunggal yang terakhir adalah simpangan baku, atau yang biasa dikenal dengan istilah
deviasi standar
. Kamu pasti pernah mendengar istilah ini, kan? Nah, simpangan baku itu adalah
akar dari ragam
. Rumusnya seperti ini, ya!

Untuk simpangan baku, gampang banget nih, buat ngapalin rumusnya. Kamu tinggal kasih akar saja pada rumus ragam, lalu selesai, deh! Kita coba
contoh soal yang sama dengan ragam tadi
, ya! Data yang kita punya adalah:
6, 7, 8, 8, 10, 9
Maka,
mean atau rata-ratanya
adalah:
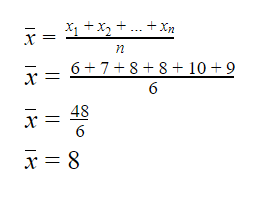
Lalu, kita hitung
simpangan bakunya
menggunakan rumus sebagai berikut:
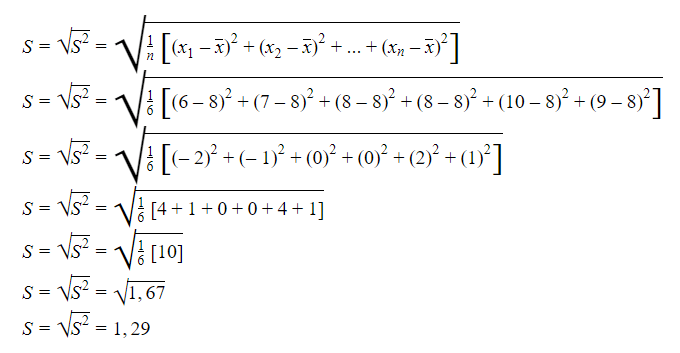
Bisa dilihat kan, kalau rumus simpangan baku itu adalah
akar dari ragam
. Karena
ragamnya adalah
1,67
, maka
simpangan bakunya adalah
1,29
. Begitu,
guys
!
Nah, sekian pembahasan kita tentang istilah-istilah statistik data tunggal. Ada
mean (rataan hitung), modus, median, jangkauan, kuartil, simpangan kuartil, simpangan rata-rata, ragam,
dan
simpangan baku
.
Hmm
.. ternyata banyak juga, ya! Apalagi rumus-rumusnya duh, bikin pusing 🙁
Eits
, tapi tenang aja! Kalau kamu pusing dan ingin bertanya lebih lanjut tentang statistika, kamu bisa tanya melalui
ruanglesonline
. Di sini, kamu bisa menanyakan berbagai soal sulit kepada guru privat berkualitas dengan hanya modal HP dan foto soal aja, lho!
Kuy
, cobain sekarang!
Referensi:
Sharma S. N., Widiastuti N., Himawan C., dkk. (2017).
Jelajah Matematika SMA Kelas XII Program Wajib
. Jakarta: Yudisthira.
Artikel ini telah diperbarui pada 21 September 2021.