
RG Squad, sebelumnya kalian telah belajar
teori peluang kejadian majemuk bagian 1
1. Dua Kejadian Saling Bebas
Kejadian A dan B dikatakan saling bebas jika kejadian A tidak mempengaruhi kejadian B dan kejadian B tidak mempengaruhi kejadian A. Dirumuskan:
P (A ∩ B) = P (A) X P (B)
Contoh:
Jika peluang Andi dapat menyelesaikan suatu soal adalah 0,4 dan peluang Budi dapat menyelesaikan soal yang sama adalah 0,3 maka peluang mereka berdua dapat menyelesaikan soal tersebut adalah …
Jawab :
P(A) = 0,4
P(B) = 0,3
Peluang Andi dan Budi dapat menyelesaikan soal:
Dua Kejadian Bersyarat
Jika kejadian A dan B tidak saling bebas, kejadian B dipengaruhi oleh kejadian A atau kejadian B dengan syarat A, dirumuskan:
Contoh:
Sebuah dadu dilempar sekali. Tentukan peluang munculnya mata dadu ganjil dengan syarat munculnya kejadian mata dadu prima lebih dahulu.
Jawab:
S = {1, 2, 3, 4, 5, 6}, n(S) = 6
A = Kejadian munculnya angka prima
A = {2, 3, 5}, n(A) = 3
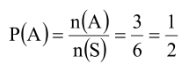
B = Kejadian muncul mata dadu ganjil
B = {1, 3, 5}
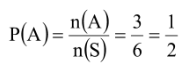
Peluang munculnya mata dadu ganjil dengan syarat munculnya kejadian mata dadu prima lebih dahulu:
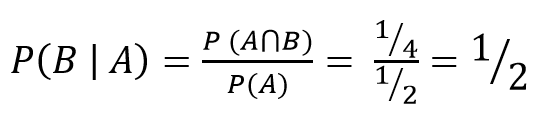
Setelah mempelajari seluruh peluang kejadian majemuk, maka dapat disimpulkan:
Kali ini RG Squad telah selesai belajar tentang teori peluang, yaitu mengenai
aturan perkalian dan faktorial
,
permutasi
,
kombinasi dan Binomial Newton
,
percobaan ruang sampel dan peluang suatu kejadian
, dan
peluang kejadian majemuk
.
Yuk
belajar berbagai topik dan pelajaran lainnya
di
ruangbelajar
!
Sumber Referensi
Sharma S. N, Widiastuti N, Himawan C, dkk (2017) Jelajah Matematika SMA Kelas XII Program Wajib. Jakarta:Yudisthira
Artikel diperbarui 21 Januari 2021