Cara Menyelesaikan Bentuk-Bentuk Aljabar | Matematika Kelas 7

Dalam Matematika, kita akan sering menemukan bentuk aljabar. Apakah itu dan bagaimana cara menyelesaikannya? Yuk, cari tau jawabannya di artikel ini!

—

Siapa yang pernah mendengar istilah aljabar? Aljabar merupakan

salah satu cabang ilmu matematika yang menggunakan simbol dan operasi matematika, seperti penjumlahan, pengurangan, perkalian, dan pembagian untuk pemecahan masalah.

Al-jabr berasal dari bahasa Arab yang artinya restorasi atau melengkapi. Kamu tahu siapa penemunya? Ia merupakan cendikiawan bernama Al-Khawarizmi.

Al-Khawarizmi: Penemu Aljabar (Sumber: reportasenews.com)

Baca juga:
Al-Khawarizmi, Ilmuwan Terpenting dalam Sejarah Matematika

Aljabar biasanya digunakan untuk menyelesaikan suatu permasalahan di berbagai bidang studi, seperti
matematika, kimia, biologi, ekonomi
, dan lain sebagainya. Jadi, nggak cuma di matematika aja, ya. Makanya, materi ini penting sekali untuk kamu pahami.
Sekarang, mari kita simak lebih lanjut tentang aljabar dan cara menyelesaikan bentuk-bentuknya.

Bentuk-Bentuk Aljabar

Nah, biasanya suatu permasalahan ditulis terlebih dahulu dalam bentuk aljabar agar penyelesaiannya lebih mudah. Bentuk aljabar t
erdiri dari konstanta, variabel, dan koefisien yang dihubungkan melalui operasi penjumlahan, pengurangan, perkalian, pembagian, perpangkatan, dan pengakaran. Contohnya kayak gambar berikut ini.

Kalo kamu perhatikan, bentuk aljabar di atas terdiri dari huruf x sebagai variabel, angka 2 sebagai koefisien nilai x, dan angka 5 sebagai konstanta. Konstanta adalah nilai yang tetap, jadi nilainya sudah jelas. Sementara itu, variabel adalah nilai yang belum tetap, makanya bisa berubah-ubah.

Kemudian, variabel bisa disimbolkan menggunakan huruf, misalnya a, b, c, x, y, dan lain sebagainya. Terakhir, koefisien adalah nilai yang berada di depan variabel. Suatu variabel pasti punya yang namanya koefisien, teman-teman.

Contoh bentuk aljabar lainnya, antara lain sebagai berikut:

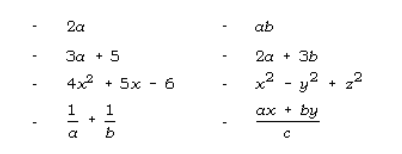
Baca juga:
Hubungan Antar Himpunan Matematika

Oh iya, selain istilah konstanta, variabel, dan koefisien, dalam aljabar, kamu juga akan menemukan istilah lain, seperti suku maupun faktor. Wah, apa tuh ya?

1. Suku, yaitu sebuah konstanta, atau variabel, atau variabel beserta koefisiennya.

Antar suku bisa digabungkan menggunakan operasi penjumlahan atau pengurangan.

Contohnya:

• 
  8, terdiri dari satu suku yang berupa konstanta.
  


• 
  9a + 2b, terdiri dari dua suku, yaitu 9a dan 2b yang dihubungkan menggunakan operasi penjumlahan.
  


• 
  3n
  
  ²
  
  – 2n – n, terdiri dari tiga suku, yaitu 3n
  
  ²
  
  , 2n, dan n yang dihubungkan menggunakan operasi pengurangan.
  

Suku bisa dibedakan menjadi suku sejenis dan suku tidak sejenis.
Dikatakan suku sejenis jika variabel dan pangkat variabelnya itu sama. Tapi, jika keduanya berbeda, disebut dengan suku tidak sejenis.

Contohnya:

• 
  2p
  
  ²
  
  q + 5p
  
  ²
  
  q disebut suku sejenis karena variabel dan pangkat variabelnya sama.
  


• 
  2xy
  
  ²
  
  + 2x
  
  ²
  
  y disebut suku tidak sejenis karena variabel dan pangkat variabelnya tidak sama.
  

2. Faktor adalah bilangan yang membagi habis bilangan lain.

Contohnya:
m × n × o atau m⋅n⋅o,
faktornya adalah m, n, dan o.

Baca juga:
Mengenal Operasi Hitung pada Pecahan

Operasi Hitung Aljabar

Oke, setelah kamu mengetahui bentuk dan istilah dalam aljabar, sekarang kita masuk ke cara menyelesaikan operasi bentuk aljabar, ya. Kita bahas tiga operasi bentuk aljabar terlebih dahulu, yaitu penjumlahan, pengurangan, dan perkalian. Yuk, langsung aja kita simak!

1. Penjumlahan bentuk aljabar

Syarat suatu aljabar bisa dijumlahkan adalah suku-sukunya harus sejenis. Hayo, masih ingat kan dengan pengertian suku sejenis? Nah, supaya kamu lebih paham, kita coba kerjakan beberapa contoh soal berikut, ya.

Contoh soal:

Sederhanakan bentuk dari 5a – 2b + 6a + 4b – 3c.

Penyelesaiannya mudah, kok. Kita hanya perlu menyusun atau mengelompokkan suku-suku yang sejenis. Suku sejenis berarti variabelnya harus sama. Setelah dikelompokkan, kita bisa jumlahkan aja koefisiennya.

5a – 2b + 6a + 4b – 3c

=
5a + 6a
– 2b + 4b
– 3c

= (5 + 6)a + (-2 + 4)b – 3c

= 11a + 2b – 3c

2. Pengurangan bentuk aljabar

Sama seperti operasi penjumlahan aljabar, kita hanya bisa melakukan operasi pengurangan aljabar jika suku-sukunya sejenis.
Contohnya:

Kurangkan 9a – 3 dari 13a + 7.

(13a + 7) – (9a – 3)

= 13a + 7 – 9a + 3

=
13a – 9a
+ 7 + 3

= (13 – 9)a + 10

= 4a + 10

Sejauh ini paham, ya? Nah, selain cara-cara di atas, kita juga bisa loh menyelesaikan operasi penjumlahan dan pengurangan aljabar menggunakan lajur atau kolom suku yang sejenis. Contohnya kayak beberapa soal berikut ini!

3. Penjumlahan dan pengurangan bentuk aljabar menurut lajur atau kolom suku sejenis

Pada soal berikut, kita tinggal menyusun suku-suku aljabar sesuai dengan variabelnya yang sejenis, ya.

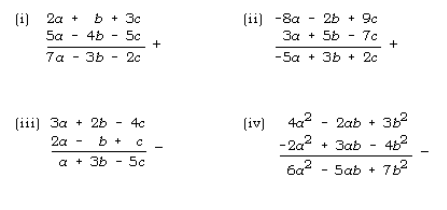
Oke, supaya kamu semakin paham dengan materi penjumlahan dan pengurangan aljabar, coba deh, jawab quizz di bawah ini!

4. Perkalian Bentuk Aljabar

Kita lanjut ke operasi perkalian pada aljabar, ya. Berbeda dengan operasi penjumlahan dan pengurangan yang hanya bisa diselesaikan jika suku-sukunya sejenis, untuk operasi perkalian ini, dapat diselesaikan, baik sukunya sejenis, maupun tidak sejenis.

Oh iya, pada aljabar, simbol perkalian ditulis dengan “×”, “⋅”, ataupun hanya dipisah dengan tanda kurung aja “( )( )”. Operasi perkalian bentuk aljabar bisa kita selesaikan menggunakan metode distributif. Hayo, ada yang masih ingat nggak?

a. Perkalian aljabar antara suku satu dengan suku dua

Jadi, menurut metode distributif, kita tinggal mengalikan a terhadap b, dan a terhadap c. Distributif perkalian terhadap penjumlahan dan pengurangan:

Penjumlahan: a × (b + c) = ab + ac

Pengurangan: a × (b – c) = ab – ac

Contohnya:

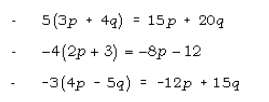
b. Perkalian aljabar antar suku dua

Kurang lebih konsepnya sama nih dengan poin a, untuk perkalian antar suku dua menggunakan metode distributif, kita kalikan aja a terhadap c, a terhadap d, b terhadap c, dan b terhadap d.

(a +
b)(c + d) = ac + ad + bc + bd

Contohnya:

Selesaikan perkalian bentuk aljabar (2x + y)(5x – 3y)

(2x + y)(5x – 3y)

= (2x)(5x) + (2x)(-3y) + (y)(5x) + (y)(-3y)

= 10x

²

+ (-6xy) + 5xy + (-3y

²

)

= 10x

²

– 6xy + 5xy – 3y

²

= 10x

²

– 1xy – 3y

²

= 10x

²

– xy – 3y

²

Gimana nih, teman-teman? Kamu sudah mulai bisa memahami tentang pendefinisian dan operasi hitung aljabar, bukan? Kalau masih ada yang dirasa bingung, tuliskan pertanyaanmu di kolom komentar ya. Nah, jika kamu mau belajar langsung sama yang ahlinya, juga boleh,

lho

. Gabung sekarang di
ruangles
untuk

#BelajarJadiHebat

.

Referensi:

As’ari A.R., Tohir M., Valentino E., Imron Z., Taufiq I. (2017).

Matematika SMP/MTs Kelas VII Semester I

. Jakarta: Pusat Kurikulum dan Perbukuan, Balitbang, Kemendikbud.

Sumber Foto:

Foto ‘Al-Khawarizmi’ [Daring]. Tautan: http://reportasenews.com/muhammad-al-khwarizmi-bapak-matematika-aljabar-dan-algoritma/ (Diakses: 21 Desember 2020)

Artikel ini telah diperbarui pada 21 Desember 2020.