Artikel ini membahas mengenai operasi suku banyak, konsep sisa dan pembagian menggunakan cara horner
Hai guys siapa nih diantara kalian yang pernah ngajarin adiknya operasi bilangan?
Kamu masih inget
nggak
? itu loh penjumlahan, pengurangan, perkalian dan pembagian. “Ohhh, kalau itu saya inget banget kak, karena sampe sekarang aja masih sering dipakai”
Yap betul banget! sebenarnya kamu udah ketemu operasi bilangan dari SD, dan waktu SMP kelas 7 kamu juga mulai belajar operasi aljabar kan? Jadi, setiap jenjang studi sebenarnya berkaitan dengan operasi bilangan ataupun aljabar, alasannya sederhana karena kita menerapkannya di kehidupan sehari-hari.
Di jenjang SMA kita bakal belajar operasi aljabar lagi, tapi agak beda
nih
. Karena yang akan dibahas kali ini mengenai operasi suku banyak.
Eits
, kamu udah paham konsep awal dari suku banyak belum? Kalo masih bingung tentang konsep dan cara mencari nilai suku banyak, kamu baca ini dulu
deh
Mempelajari Konsep dan Nilai Suku Banyak
.
Materi ini seru banget untuk dipelajari, karena kita
nggak
cuma belajar tentang operasinya tapi konsep sisa dan juga pembagian yang
nggak
biasa (karena dengan bantuan Horner!)
so
, supaya pemahaman kamu tentang suku banyak ini makin mantap, wajib baca sampai habis ya!

Seperti operasi aljabar pada umumnya, operasi suku banyak terdiri dari penjumlahan, pengurangan, perkalian dan pembagian. Khusus untuk pembagian, akan dijelaskan dengan cara biasa yaitu bersusun ke bawah dan menggunakan cara Horner. Kita bahas satu per satu
yuk!

Aturan dari penjumlahan suku banyak adalah
menjumlahkan suku yang memiliki variabel serta eksponen yang sama atau menjumlahkan suku sejenis.
Penjumlahan suku banyak akan menghasilkan suku banyak dengan eksponen yang sama. Misalnya ini:

Contoh Soal:
Jika f(x) = 2x
3
+ 4x
2
+ 6x + 8 dan g(x) = 7x
2
– 9x – 11maka hasil dari f(x) + g(x)=…
Pembahasan:
f(x) +g(x) = (2x
3
+ 4x
2
+ 6x + 8) + (7x
2
– 9x – 11)
= 2x
3
+ (4 + 7)x
2
+ (6 – 9)x + 8 -11
= 2x
3
+ 11x
2
– 3x – 3
Jadi hasil penjumlahan f(x) dan g(x)adalah 2x
3
+ 11x
2
– 3x – 3.

Pengurangan suku banyak artinya,
mengurangkan suku dengan variabel dan eksponen yang sama atau mengubah tanda fungsi yang dikurangi. Sebenarnya, aturan pegurangan sama dengan penjumlahan, letak perbedaanya hanya pada operasinya saja.
Tapi, kamu harus teliti untuk tanda plus dan minusnya ya!
Contoh Soal:
Diketahui f(x) = 5x
4
+ 7x
2
– 3x + 5 dan g(x) = 4x
4
– 8x
3
+ 2x + 10, tentukan hasil dari f(x) -g(x)!
Pembahasan:
f(x) – g(x) = (5x
4
+ 7x
2
– 3x + 5) – (4x
4
– 8x
3
+ 2x + 10)
= (5 – 4)x
4
– (- 8x
3
) + 7x
2
+ (- 3 – 2)x + 5 – 10
= x
4
+ 8x
3
+ 7x
2
– 5x – 5
Ingat!
untuk
susunan hasilnya
dimulai dari eksponen tertinggi hingga terendah
.

Mengalikan satu per satu suku yang ada, hingga memperoleh eksponen yang lebih tinggi atau kita menggunakan sifat distributif.
Kalo kamu lupa, sifat distributif itu misalnya
kaya gini
:

Udah lebih ingat kan sekarang? Kalo gitu langsung ke contoh soal aja ya!
Contoh Soal:
Tentukan hasil dari perkalian dua suku banyak ini (2x
2
+ 6)(x
3
– x + 2)!
Pembahasan:
Kamu bisa menggunakan sifat distributif, seperti ini
(2x
2
)(x
3
) + (2x
2
)(-x) + (2x
2
)(2)+(6)(x
3
) + (6)(-x)+(6)(2)
= 2x
2+3
– 2x
2+1
+ 4x
2+0
+ 6x
3
– 6x+12
= 2x
5
– 2x
3
+ 4x
2
+ 6x
3
– 6x+12
= 2x
5
+ (-2+6)x
3
+ 4x
2
– 6x+12
= 2x
5
+ 4x
3
+ 4x
2
– 6x+12
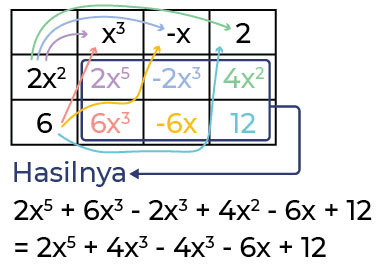
Atau kamu juga bisa coba dengan tabel seperti ini:

Seperti yang sudah disinggung sebelumnya,
pembagian suku banyak bisa menggunakan cara bersusun dan Horner.
Untuk cara Horner, sudah sempat dibahas dan dipakai untuk mendapatkan nilai suku banyak, tapi tenang aja untuk operasi pembagiannya bakal dibahas kok disini. Sebelum ke contoh soal, kamu harus tahu hubungan suku yang akan dibagi, pembagi dan lainnya, seperti ini:

Contoh Soal Pembagian Cara Horner:
Tentukan hasil bagi Tentukan hasil bagi f(x) = x
3
– 9x + 14 dengan x-3 dengan sintetik Horner!
step 1:
Tuliskan koefisien yang dibagi yaitu 1, 0 (karena x
2
tidak ada dalam soal maka sama dengan 0x
2
),-9 dan 14 dengan pembagi yaitu 3.
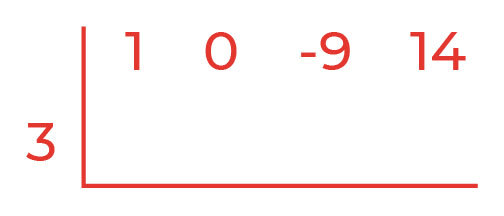
step 2:
Tulis koefisien suku pertama yaitu 1 di daerah hasil atau baris ke-3
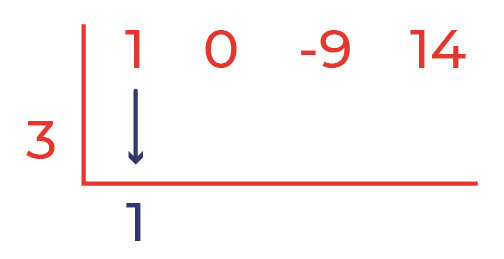
step 3:
Kalikan 3 dengan hasil dari step 2 yaitu 1 dan letakkan hasilnya yaitu 3 di kolom 2 baris 2. Jangan lupa jumlahkan angka 0 (koefisien suku 2) dengan 3 (hasil dari perkalian 3 dan 1) letakkan hasilnya di daerah hasil atau kolom 2 baris 3.
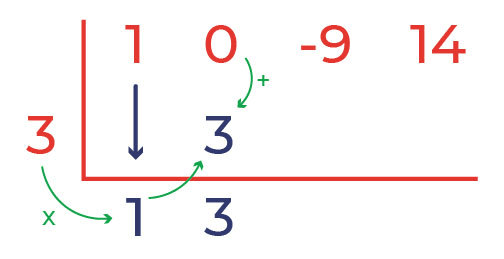
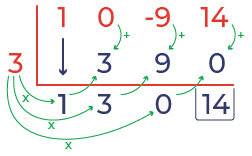
Ulangi step ke 3 sampai memperoleh angka paling akhir di daerah hasil.
Langkah terakhir, kita menentukan
hasil bagi dan juga sisanya
. Kita lihat pada daerah hasil 1, 3, 0 merupakan koefisien dari variabel x dengan derajat menurun. Sedangkan 14 adalah sisa, jadi seperti ini :
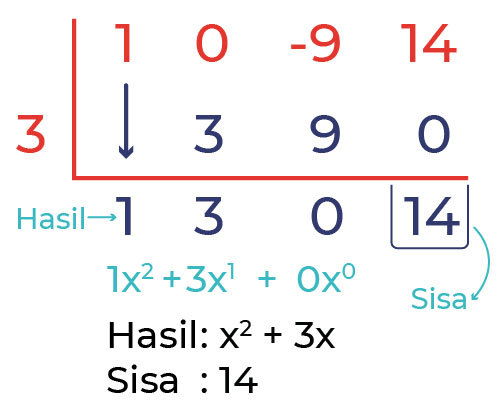
Maka, hasil bagi f(x) = x
3
– 9x + 14 dengan x-3 menggunakan cara Horner adalah x
2
+ 3xdengan sisa 14.
Next,
langsung aja yuk kita bahas cara bersusun!
Pembagian cara bersusun mirip banget konsepnya dengan pembagian bilangan waktu kita SD dulu
.
Contoh Soal Pembagian Bersusun :
Hasil bagi f(x) = x
3
– 9x + 14 dengan x-3 dengan cara bersusun adalah…
step 1:
Susun kedua suku banyak x
3
– 9x + 14 (yang kita sebut dengan “terbagi”) dengan x-3 (yang kita sebut dengan “pembagi”) tersebut menjadi seperti ini.
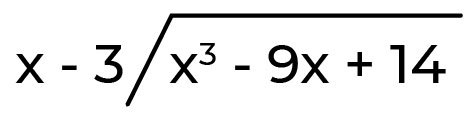
step 2:
Bagi suku pertama terbagi yaitu x
3
dengan suku pertama pembagi yaitu x.
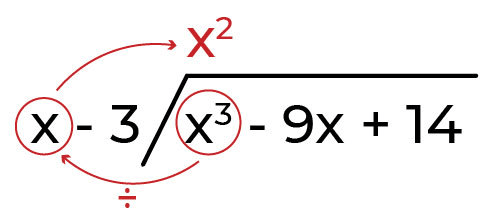
step 3:
Kalikan x
2
(hasil bagi dari step 2) dengan pembagi yaitu x-3, hasilnya ditaruh di baris ke-2. Kurangkan hasil yang diperoleh dan letakan hasil di bawahnya.
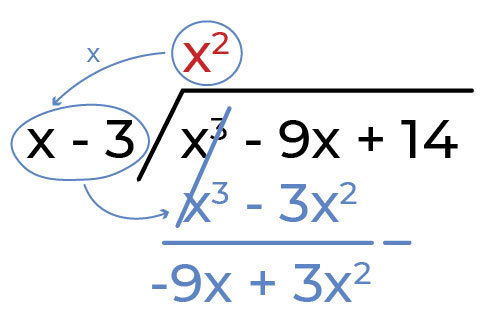
step 4:
Bagi -9x ( hasil dari pengurangan step 3) dengan x (suku pertama pembagi)
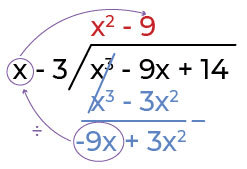
step 5:
Kalikan hasil dari step 4 yaitu -9 dengan pembagi yaitu x-3. Letakan hasilnya di bawah -9x + 3x
2
(hasil pengurangan step 3).
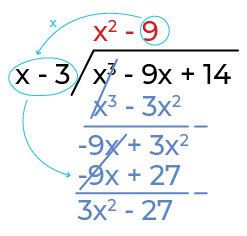
Lakukan berulang step 2-5 hingga tidak ada lagi variabel yang dapat dibagi dan hanya menyisakan konstantanya yaitu 14.
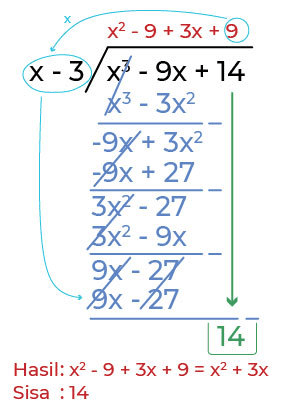
Jadi, hasil bagi x
3
– 9x + 14 dengan x-
3
adalah x
2
+ 3x dengan sisanya yaitu 14.
Oke,dari perhitungan fungsi yang tadi, kita mendapatkan sisa pembagian kan?
Nah,
kamu tahu nggak
sih
maksud dari konsep sisa? Langsung aja deh kita bahas!
Baca Juga:
Mengulik Materi Logika Matematika: Konvers, Invers, dan Kontraposisi

Jadi pada
konsep sisa ini, kita bisa mengetahui sisa hasil bagi secara langsung tanpa melakukan pembagian terlebih dahulu,
wah jadi lebih mudah yaa! dari bentuk umum yang sudah dibahas sebelumnya yaitu:
f(x)=P(x) . H(x) + S
Jika f(x) berderajat n, P(x) berderajat m (m ≤ n) maka derajat H(x) dan S masing-masing :
derajat H(x) adalah (n-m)
derajat maksimum S adalah (m-1)

Contoh soal:
Tentukan sisa hasil bagi f(x) = x
3
– 9x + 14 oleh x-3!
Pembahasan:
Sesuai konsep sisa, f(x) yang dibagi dengan (x-k) sisanya atau S = f(k). Maka (x-k) ⇨(x-3)
Jadi nilai k = 3, substitusikan k = 3 ke f(x) = x
3
– 9x + 14
f(3) = 3
3
– 9(3) + 14
= 27 – 27 + 14
= 14
Kalau kita lihat hasil sisa pembagian menggunakan cara horner atau pembagian biasa hasilnya sama yaitu 14. Tapi untuk mencari nilai sisa, kalo pakai konsep sisa jauh lebih cepat.
Gimana
nih
udah lebih paham kan sekarang materi tentang operasi suku banyak dan konsep sisa ? Atau kamu masih mau latihan soal lagi buat menambah kemampuan kamu?
Tenang
guys
, aku punya solusinya! Sekarang kamu gabung ke
ruangbelajar
deh! Di sana kamu bisa latihan soal sepuasnya ditambah lagi pembahasan yang mudah dipahami dan pastinya bikin kamu makin semangat untuk belajar!
Referensi:
Wirodikromo, S. (2007) Matematika Jilid 2 IPA untuk kelas XI. Jakarta: Erlangga.