
Belajar tentang
logika matematika
, yuk! Mulai dari pengertian kalimat terbuka, pernyataan dan negasi, serta pernyataan majemuk (konjungsi, disjungsi, implikasi, dan biimplikasi).
—
Teman-teman, apa yang kamu bayangkan ketika mendengar tentang
logika matematika
? Kalau kamu murid laki-laki, mungkin akan bingung dan bertanya, “
Kok
matematika pakai logika segala?”. Sementara sebagian perempuan akan berpikir, “Logika itu mah urusan laki-laki! Perempuan
tuh
pake
nya perasaan…”
Hmmm…
Di dalam ilmu matematika, kamu juga dapat mempelajari logika. Buat apa? Tentu aja, buat mengasah otak kita dalam penarikan kesimpulan-kesimpulan. Jadi, ke depannya kita tidak asal menduga sesuatu. Tidak ada lagi deh, kalimat “Kamu bilangnya mau jemput jam 10.
Kok
telat? Pasti JALAN SAMA MANTAN YA?!”
Nah, dalam materi logika matematika, kita akan sering menemukan istilah-istilah, seperti negasi, konjungsi, disjungsi, dan lain sebagainya. Di
artikel Matematika kelas 11
kali ini, kita akan bahas secara mudah dan ringkas, ya. Yuk, perhatikan secara seksama!
Pernyataan dan Kalimat Terbuka
Coba kamu perhatikan gambar berikut!

Hayo, dari gambar di atas, tahu nggak bedanya
pernyataan dan kalimat terbuka
?
Pernyataan adalah kalimat yang bisa benar atau bisa salah
. Sementara
kalimat terbuka adalah jenis kalimat yang belum diketahui kebenarannya
. Sehingga, untuk menentukan benar atau salahnya, kita perlu pengamatan lebih lanjut.
Baca Juga:
Cara Mencari Determinan dan Invers Matriks
—
Sudah tahu belum, di Aplikasi belajar Ruangguru, ada fitur Drill Soal yang berisi kumpulan contoh soal latihan beserta pembahasannya, loh. Pas banget kan buat mempersiapkan diri kamu dalam menghadapi ujian nanti. Yuk, klik banner di bawah ini untuk coba fitur Drill Soal!
Kalau kamu masih bingung seperti apa itu
contoh pernyataan
, berikut adalah salah satu contohnya:
Indonesia Raya adalah lagu kebangsaan Indonesia. (pernyataan
benar
)
Bika ambon berasal dari Ambon. (pernyataan
salah
)
Di sisi lain,
contoh dari kalimat terbuka
adalah sebagai berikut:
12x + 6 = 91 (pernyataan ini dinamakan kalimat terbuka karena
masih harus dibuktikan kebenarannya
. Apakah benar 12x jika dijumlahkan dengan 6 akan menghasilkan 91?)
Maaf ya, aku semalem ketiduran. Hehehe. (Pernyataan ini dinamakan kalimat terbuka karena
masih harus dibuktikan kebenarannya
. Apakah benar dia semalem nggak bales
chat
karena ketiduran? Atau emang males aja
chat
sama kamu?)
Nah, setelah mengetahui apa itu pernyataan dan kalimat terbuka, sekarang kita lanjut pembahasan mengenai ingkaran atau disebut juga dengan negasi atau penyangkalan.
Ingkaran atau Negasi atau Penyangkalan (~)
Dari sebuah pernyataan, kita dapat membuat pernyataan baru berupa
ingkaran atau negasi
, yakni penyangkalan atas pernyataan tadi. Untuk lebih memahami hal ini, perhatikan
tabel kebenaran ingkaran
berikut:
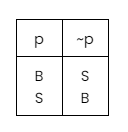
Keterangan:
B = pernyataan bernilai benar
S = pernyataan bernilai salah
Artinya,
jika suatu pertanyaan (p) benar, maka ingkaran (q) akan bernilai salah
. Begitu pula sebaliknya. Nah, negasi ini dilambangkan dengan lambang garis seperti ini:
~
Contoh negasi dalam matematika
yaitu seperti berikut:
p: Besi memuai jika dipanaskan (pernyataan bernilai
benar
)
~p: Besi
tidak
memuai jika dipanaskan (pernyataan bernilai
salah
).
Contoh lain:
p:
Semua
unggas
adalah
burung.
~p:
Ada
unggas yang
bukan
burung.
Dalam kehidupan sehari-hari, kita seringkali menemui orang menggunakan pernyataan negasi atas pernyataan orang lain… yang akhirnya bisa berujung pada pertengkaran. Contohnya seperti gambar di bawah ini, nih!

Baca Juga:
Konsep Limit Fungsi Aljabar dan Sifat-Sifatnya
Oke, kembali fokus. Sudah mengerti tentang ingkaran atau negasi, kan? Selanjutnya, kita akan mempelajari tentang pernyataan majemuk.
Apa itu pernyataan majemuk
?

Pernyataan Majemuk
Dalam ilmu matematika, terdapat
4 macam
pernyataan majemuk, yaitu
konjungsi
,
disjungsi
,
implikasi
, dan
biimplikasi
. Yuk, kita bahas satu per satu!
Konjungsi (∧)
Konjungsi adalah
pernyataan majemuk dengan kata hubung
“
dan
”. Sehingga, notasi “
p ∧ q
” dibaca “
p dan q
”. Berikut adalah
tabel nilai kebenaran k
onjungsi
.

Dari tabel di atas, kita dapat melihat bahwa
konjungsi hanya akan benar
jika kedua pernyataan (p dan q) benar
.
Contoh konjungsi
:
p: 3 adalah bilangan prima (pernyataan bernilai benar)
q: 3 adalah bilangan ganjil (pernyataan bernilai benar)
p ∧ q: 3 adalah bilangan prima
dan
ganjil (pernyataan bernilai benar)
—
Sampai sini, mulai paham kan tentang materi Logika Matematika yang satu ini? Atau kamu jadi keinget punya PR yang kamu masih kurang pahamin? Gampang, kamu bisa banget langsung kirim foto soal PR kamu, dan penjelasannya di
roboguru
! Cobain langsung dengan klik banner roboguru dibawah ini ya!
Disjungsi (∨)
Disjungsi adalah
perny
ataan majemuk dengan kata hubung “atau”
. Sehingga notasi “
p ∨ q
” dibaca “
p atau q
”. Berikut adalah
t
abel nilai kebenaran disjungsi
.

Jika kita lihat pada tabel kebenaran, disjungsi
hanya salah jika kedua pernyataan (p dan q) salah
.
Contoh disjungsi
:
p: Paus adalah mamalia (pernyataan bernilai benar)
q: Paus adalah herbivora (pernyataan bernilai salah)
p ∨ q: Paus adalah mamalia
atau
herbivora (pernyataan bernilai benar)
Implikasi (⇒)
Implikasi adalah
pernyataan majemuk dengan kata hubung
“
jika… maka…
” Sehingga notasi dari “
p ⇒ q
” dibaca “
Jika p, maka q
”. Adapun
tabel nilai kebenaran dari implikasi
yaitu sebagai berikut.

Dari tabel terlihat bahwa implikasi
hanya bernilai salah jika anteseden (p) benar, dan konsekuen (q) salah
.
Baca Juga:
4 Metode Pembuktian Matematika
Contoh implikasi
:
p: Andi belajar dengan aplikasi ruangguru. (pernyataan bernilai benar)
q: Andi dapat belajar di mana saja. (pernyataan bernilai benar)
p ⇒ q:
Jika
Andi belajar dengan aplikasi ruangguru
,
maka
Andi dapat belajar dari mana saja (pernyataan bernilai benar)
Biimplikasi (⇔)
Biimplikasi adalah
pernyataan majemuk dengan kata hubung “… jika dan hanya jika”
. Sehingga, notasi dari “
p ⇔ q
” akan dibaca “
p jika dan hanya jika q
”.
Adapun
tabel nilai kebenaran dari biimplikasi
yaitu sebagai berikut.

Dari tabel kebenaran tersebut, dapat kita amati bahwa
biimplikasi akan bernilai benar jika sebab dan akibatnya (pernyataan p dan q) bernilai sama
.
Baik itu sama-sama benar, atau sama-sama salah.
Contoh biimplikasi
:
p: 30 x 2 = 60 (pernyataan bernilai benar)
q: 60 adalah bilangan ganjil (pernyataan bernilai salah)
p ⇔ q: 30 x 2 = 60
jika dan hanya jika
60 adalah bilangan ganjil (pernyataan bernilai salah).
—
Nah
, itu tadi penjelasan tentang
logika matematika
, baik dalam penggunaan pernyataan dan kalimat terbuka, ingkaran, serta 4 macam kalimat majemuk (konjungsi, disjungsi, implikasi, dan biimplikasi).
Kalau kamu ingin memahami materi seperti ini sambil menonton video penjelasan beranimasi lengkap dengan rangkuman infografis dan latihan soal, langsung aja daftar di
ruangbelajar
!
Referensi:
Sharma S. N., Widiastuti N., Himawan C., dkk. (2017).
Jelajah Matematika SMA Kelas XI Program Wajib
. Jakarta: Yudisthira.
Artikel ini telah diperbarui pada 9 Mei 2023.