
Artikel Matematika kelas 10
ini akan menjelaskan tentang cara menyelesaikan bentuk persamaan dan pertidaksamaan eksponen, disertai dengan beberapa contoh soalnya. Yuk, kita belajar bersama!
—
Guys, dalam mempelajari matematika, mungkin kamu sudah tidak asing lagi dengan cara menyelesaikan bentuk persamaan maupun pertidaksamaan, ya. Mulai dari cara menyelesaikan
persamaan atau pertidaksamaan linear
,
persamaan atau pertidaksamaan kuadrat
,
persamaan atau pertidaksamaan trigonometri
, dan masih banyak lagi.
Sebenarnya, hal yang membedakan antara bentuk persamaan dengan pertidaksamaan hanya terletak pada tanda penghubungnya saja,
nih
. Kalau persamaan dihubungkan dengan tanda “=”, sedangkan pertidaksamaan dihubungkan dengan tanda “<, >, ≤, ≥, atau ≠”.
“Berbeda tanda penghubungnya, tentu berbeda pula nama dan cara penyelesaiannya.”
Nah
, pada artikel kali ini, kamu akan mempelajari bagaimana cara menyelesaikan persamaan maupun pertidaksamaan eksponen.
Wow
, penasaran
nggak sih
gimana caranya?
Yuk
, langsung saja kita simak!
Persamaan Eksponen
Kita mulai dari persamaan eksponen dulu, ya. Menurut definisinya,
persamaan eksponen
adalah persamaan yang pangkatnya atau bilangan pokok (basis) dan pangkatnya memuat suatu variabel
.
Hah? hah? gimana? gimana? (sumber: giphy.com)
Oke, supaya kamu
nggak
bingung, coba kamu perhatikan dua contoh di bawah ini,
deh
.
Contoh Persamaan Eksponen
1. 3
2x-3
= 81
x+5
→ persamaan eksponen dengan
pangkat mengandung variabel x
2. (2x – 5)
x
= (2x – 5)
3x-4
→ persamaan eksponen dengan
basis dan pangkat mengandung variabel x
Jadi, dalam persamaan eksponen itu, bisa pangkatnya saja yang mengandung variabel atau bisa juga basis dan pangkatnya yang mengandung variabel.
Variabel ini dilambangkan dengan huruf
, bisa dari a sampai dengan z.
Tapi, pada umumnya, lambang variabel yang sering digunakan di soal adalah huruf x. Gimana? Sekarang, sudah kebayang
kan
bentuk persamaan eksponen itu seperti apa?
Lalu, bagaimana cara menyelesaikannya?
Penyelesaian persamaan eksponen merupakan himpunan semua nilai x yang memenuhi persamaan eksponen tersebut
, atau bisa juga kita sebut sebagai himpunan penyelesaian.
Nah
, cara menyelesaikan persamaan eksponen itu berbeda-beda, tergantung bentuk persamaannya.
Dua contoh persamaan di atas tadi adalah dua dari beberapa bentuk persamaan eksponen yang ada. Artinya, masih ada bentuk-bentuk persamaan eksponen yang lain dan setiap persamaan memiliki cara penyelesaiannya sendiri.
Tapi, kamu nggak perlu khawatir, artikel ini telah merangkum semua bentuk persamaan eksponen beserta cara penyelesaiannya,
lho
. Oleh karena itu, simak terus ya.
Baca Juga:
Mengenal Logaritma, Sifat-Sifat, dan Contohnya
Bentuk-Bentuk Persamaan Eksponen
Perlu kamu ketahui, persamaan eksponen terbagi menjadi dua jenis, yaitu persamaan eksponen sederhana dan persamaan eksponen tidak sederhana. Kira-kira, apa
sih
bedanya persamaan yang sederhana dan tidak sederhana ini?
Yuk
, kita lihat penjabarannya pada gambar berikut.

Kamu dapat perhatikan, bentuk umum persamaan eksponen tidak sederhana adalah persamaan kuadrat, sehingga penyelesaian bentuk persamaan ini sedikit lebih rumit dibandingkan dengan persamaan eksponen sederhana. Oke, supaya kamu
nggak
semakin bingung, kita coba kerjakan beberapa contoh soal di bawah ini, ya.
Cara Menyelesaikan Persamaan Eksponen
Contoh soal:
Tentukanlah himpunan penyelesaian dari soal berikut ini:
1. 3
3x-2
= 81
2. 2
2x+1
– 2
x
– 6 = 0
Penyelesaian:
1. Soal nomor 1 merupakan bentuk persamaan eksponen sederhana. Kalau kamu perhatikan dari bentuk persamaannya, kira-kira mirip dengan persamaan eksponen nomor berapa, ya?
Yap
, tepat, mirip dengan bentuk persamaan eksponen nomor 2.
Jadi, himpunan penyelesaian soal nomor 1 dapat dicari dengan
menyamakan pangkat ruas kiri dengan ruas kanan
. Sehingga, penyelesaiannya akan menjadi seperti berikut:
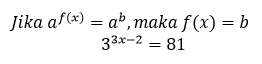
Selanjutnya, kita samakan basis antara ruas kiri dengan ruas kanan. Karena basis pada ruas kiri adalah 3, maka kita ubah 81 menjadi 3
4
.
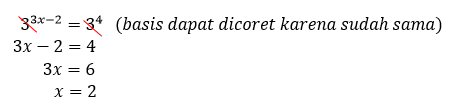
Jadi, himpunan penyelesaian dari persamaan eksponen tersebut adalah x = 2.
2. Mudah ya, guys? Kalau gitu, kita lanjut ke soal berikutnya. Soal nomor 2 merupakan bentuk persamaan eksponen tidak sederhana karena kalau kita uraikan akan membentuk persamaan kuadrat.
Langkah penyelesaian soal nomor 2 ini dapat kamu lihat pada penjelasan berikut:

Untuk menguraikan pangkat persamaan tersebut, kita gunakan
sifat-sifat eksponen
ya. Kemudian, setelah kita dapatkan nilai y, kita ubah kembali ke bentuk 2
x
, sehingga:

Jadi, himpunan penyelesaian dari persamaan eksponen tersebut adalah x = 1.
Sampai sini ada pertanyaan? Tenang, bagi kamu yang punya banyak pertanyaan, silahkan tulis pertanyaanmu di kolom komentar. Oke? Sekarang, kita lanjut ke materi berikutnya ya, yaitu pertidaksamaan eksponen. Masih kuat,
kan
?
Baca Juga:
Bentuk-Bentuk Persamaan Logaritma dan Cara Menyelesaikannya
Pertidaksamaan Eksponen
Nah
, seperti yang sudah dijelaskan sebelumnya, hal yang membedakan bentuk persamaan dengan bentuk pertidaksamaan adalah tanda penghubungnya saja.
Pertidaksamaan eksponen adalah bentuk lain dari persamaan eksponen, namun tanda penghubungnya menggunakan tanda pertidaksamaan
.
Jadi sebenarnya, bentuk-bentuk persamaan eksponen yang sudah dijabarkan di atas tadi juga merupakan bentuk pertidaksamaan eksponen, ya. Tapi, tanda penghubungnya berubah menjadi “<, >, ≤, ≥, atau ≠”.
Lalu, apakah solusi penyelesaiannya juga sama? Oh tentu saja sama. Hanya ada satu hal penting yang perlu kamu perhatikan sebelum mengerjakan pertidaksamaan eksponen. Apakah itu?
Let’s check the picture below
!
Sifat-Sifat Pertidaksamaan Eksponen

Jadi, yang perlu kamu perhatikan adalah nilai basisya. Intinya, kalau
basisnya > 1
, maka
tanda pertidaksamaannya tetap
. Sebaliknya, kalau
basisnya pecahan (0<basis>1)
, maka
tanda pertidaksamaannya berubah
, misalnya dari “<” jadi “>”, atau “≤” jadi “≥”, atau sebaliknya.
Oke, supaya kamu semakin paham, di bawah ini ada contoh soal pertidaksamaan eksponen. Kita kerjakan sama-sama, ya.
Cara Menyelesaikan Pertidaksamaan Eksponen
Contoh soal:
Tentukan penyelesaian dari pertidaksamaan 2
2x+3
> 8
x-5
!
Penyelesaian:
Ingat!
Karena kita ingin menyelesaikan bentuk pertidaksamaan eksponen, maka hal yang perlu kamu
perhatikan
lebih dulu adalah
nilai basisnya
, apakah bernilai lebih dari 1 atau antara 0 sampai 1.
Jika kita uraikan soalnya terlebih dahulu, maka diperoleh nilai basisnya, yaitu 2. Sehingga, tanda pertidaksamaannya tetap. Penjelasan lebih lengkapnya bisa kamu lihat di bawah ini:

Jadi, himpunan penyelesaian dari pertidaksamaan eksponen tersebut adalah x < 18.
—
kamu tahu
nggak
,
sih
? Sebenarnya, kunci agar pandai dalam matematika itu hanya ada dua,
lho
. Pertama, kamu harus paham dengan rumusnya.
Ingat!
hafal sama paham itu beda, ya.
Setelah itu, kamu juga harus banyak berlatih soal. Gunanya apa,
sih
? Latihan soal ternyata penting banget
lho
untuk mengasah analisa berpikir kamu. Semakin banyak jenis dan tipe soal yang kamu kerjakan, tanpa sadar kemampuanmu dalam mengerjakan soal juga ikut meningkat.
Kalau kamu merasa bosan mengerjakan soal sendiri, yuk gabung aja di
ruangbelajar
. Memahami materi pelajaran jadi lebih mudah dengan mengikuti misi bersama para Master Teacher yang keren!
Sumber referensi:
Kurnia N, Sharma S.N, Saputra S. E,(2016) Jelajah Matematika SMA Kelas X Peminatan MIPA. Jakarta:Yudhistira
Artikel diperbarui pada 24 Juli 2023.