Operasi Aljabar Pada Matriks: Penjumlahan, Pengurangan & Perkalian | Matematika Kelas 11

Artikel
Matematika kelas XI
ini menjelaskan cara menyelesaikan operasi aljabar pada matriks, mulai dari menjumlahkan, mengurangkan, sampai mengalikan dua atau lebih matriks.

—

Kamu suka nonton film fiksi ilmiah? Kalo iya, kamu harus coba tonton salah satu film yang pernah terkenal di tahun 2000-an,

deh

. “The Matrix” judulnya. Singkatnya, film ini menceritakan tentang kehidupan umat manusia yang sebenarnya telah diatur dalam

matrix

, sebuah program hasil ciptaan mesin-mesin jahat yang ingin menundukkan populasi manusia. Akibatnya, perang antara mesin dengan manusia pun tidak dapat dihindarkan dan

matrix

harus segera dihancurkan.

Mantap! Keren banget

nggak


tuh

kelihatannya. Pokoknya, bagi kamu yang suka nonton film sambil mikir, “The Matrix” harus masuk

list

tontonan kamu saat senggang atau bosan.

Adegan di film The Matrix (Sumber: giphy.com)

Hmm

, ngomongin film yang judulnya

matrix

, jadi inget, di Matematika juga ada

lho

materi tentang matriks. Tapi, pengertiannya tentu beda ya dengan

matrix

yang ada di film. Kalau di Matematika,

matriks


adalah kumpulan bilangan yang disusun berdasarkan urutan baris dan kolom, serta dibatasi oleh sebuah tanda kurung

.

Nah

, kali ini, kita akan membahas materi tentang matriks, teman-teman.

Eits

! Bukan

matrix

yang ada di film “The Matrix” itu ya, melainkan matriks yang ada dalam pelajaran Matematika. Eh, eh, jangan sedih gitu

dong

denger kata Matematika. Materinya juga

nggak

kalah seru,

kok

!

Sebenarnya, di artikel sebelumnya, matriks juga sudah pernah dibahas,

nih

. Tapi, belum semuanya. Hanya sekedar pengenalan tentang matriks dan komponen-komponennya, jenis-jenis matriks, dan transpose suatu matriks saja. Jadi, buat kamu yang belum paham betul apa itu matriks, bisa baca dulu artikelnya lewat

link

di bawah ini, ya.

Baca juga:
Cari Tahu Lebih Dalam Tentang Matriks, Yuk!

Oke, berhubung penjelasan awal tentang matriks sudah dibahas, kita akan lanjut ke materi berikutnya, yaitu operasi aljabar matriks. Terdapat tiga macam bentuk operasi aljabar pada matriks, yaitu operasi penjumlahan, pengurangan, dan perkalian. Kira-kira, bagaimana ya cara menyelesaikan masing-masing operasi tersebut? Mari kita simak penjelasannya berikut ini!

Penjumlahan dan Pengurangan Matriks

Pertama, ada operasi penjumlahan dan pengurangan matriks. Kita akan bahas satu-persatu dimulai dari operasi penjumlahannya terlebih dahulu, ya.

1. Penjumlahan Matriks

Misalkan terdapat dua buah matriks, yaitu matriks A dan matriks B. Jika matriks C adalah matriks penjumlahan dari A dengan B, maka

matriks C dapat diperoleh dengan menjumlahkan setiap elemen pada matriks A yang seletak dengan setiap elemen pada matriks B

. Oleh karena itu,

syarat

agar dua atau lebih matriks dapat dijumlahkan adalah harus

memiliki ordo yang sama

.

Contoh:

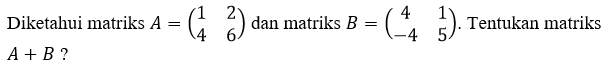
Hasil dari A + B dapat diperoleh dengan menjumlahkan setiap elemen matriks A yang seposisi dengan setiap elemen matriks B.

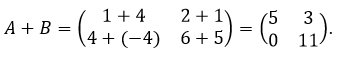
Paham, ya. Selanjutnya ada operasi pengurangan matriks. Tapi, sebelum masuk ke bahasan tentang operasi pengurangan matriks, kamu harus tahu dulu istilah tentang lawan suatu matriks.

Wadaw

! Apaan,

tuh

?!

Baca juga:
Cara Mencari Determinan dan Invers Matriks

Namanya juga lawan,

gaes

. Pasti antara matriks yang satu dengan matriks yang lain akan saling bertentangan. Gampangnya

sih

, kalau yang satu nilainya positif, pasti yang satu lagi nilainya bakal negatif. Jadi, kalau ada matriks A, maka lawan matriks A adalah suatu matriks yang elemen-elemennya merupakan lawan dari elemen-elemen matriks A tersebut.

A = [a

_ij

], lawan matriks A ditulis -A = [-a

_ij

]

2. Pengurangan Matriks

Misalkan terdapat dua buah matriks, yaitu matriks A dan matriks B. Jika matriks C adalah matriks pengurangan dari A dengan B, maka

matriks C dapat diperoleh dengan mengurangkan setiap elemen pada matriks A yang seletak dengan setiap elemen pada matriks B

.

Pada dasarnya, pengurangan sama halnya dengan penjumlahan terhadap lawan bilangan penambah, sehingga pengurangan matriks A dengan matriks B dapat diartikan sebagai penjumlahan matriks A dengan lawan matriks B.

A – B = A + (-B)

Sama halnya dengan syarat penjumlahan matriks,

dua atau lebih matriks hanya dapat dikurangkan apabila memiliki ordo yang sama

, teman-teman.

Nah

, supaya kamu

nggak

bingung, kita coba kerjakan contoh soal di bawah ini,

yuk

.

Gaasss

~

Contoh:

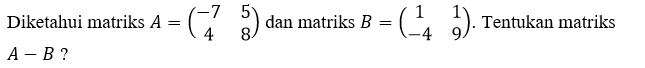
Hasil dari A – B dapat diperoleh dengan mengurangkan setiap elemen matriks A yang seposisi dengan setiap elemen matriks B.

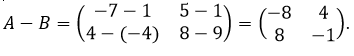
Gimana? Paham ya sampai di sini. Kalau gitu, kita lanjut ke operasi aljabar matriks berikutnya,

yok

!

Perkalian Matriks

Operasi perkalian matriks dibagi menjadi dua

nih

, yaitu perkalian matriks dengan bilangan

real

(skalar) dan perkalian antarmatriks. Kita simak pembahasan berikut untuk tahu bagaimana cara menyelesaikannya, ya.

1. Perkalian Matriks dengan Bilangan

Real

(Skalar)

Misalkan terdapat matriks A berordo m × n dan suatu bilangan

real

(skalar), yaitu k. Perkalian antara matriks A dengan skalar k dapat ditulis dengan kA yang

diperoleh dengan mengalikan setiap elemen matriks A dengan skalar k

.

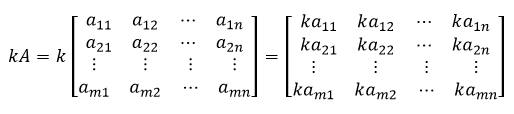
Perkalian suatu matriks dengan skalar dapat dilakukan tanpa syarat tertentu. Artinya,

semua matriks dengan ordo sembarang dapat dikalikan dengan bilangan

real

(skalar)

.

2. Perkalian Matriks dengan Matriks

Misalkan terdapat dua buah matriks, yaitu matriks A dengan ordo m × p dan matriks B dengan ordo p × n. Perkalian matriks A dengan matriks B dapat ditulis dengan A × B yang

diperoleh dari penjumlahan hasil kali elemen-elemen yang bersesuaian pada baris ke-i matriks A dengan kolom ke-j matriks B

, dengan i = 1, 2, 3, …, m dan j = 1, 2, 3, …, n.

Syarat


agar dua buah matriks dapat dikalikan adalah matriks pertama harus memiliki jumlah kolom yang sama dengan jumlah baris pada matriks kedua

. Ordo matriks hasil perkalian dua buah matriks adalah jumlah baris pertama dikali jumlah kolom ke dua.

Hmm

… Pasti kamu bingung ya maksudnya gimana. Oke, supaya kamu

nggak

bingung, kita coba kerjakan soal di bawah ini,

yuks

!

Contoh:

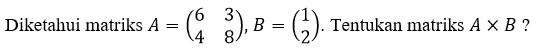
Jumlah kolom matriks A adalah 2 dan jumlah baris matriks B adalah 2. Matriks A memiliki jumlah kolom yang sama dengan jumlah baris matriks B, sehingga syarat perkalian antarmatriks sudah terpenuhi.

Selanjutnya, kita dapat mengalikan setiap elemen baris di matriks A dengan setiap elemen kolom di matriks B. Coba kamu perhatikan lingkaran berwarna pada tiap-tiap elemen matriks di bawah ini, ya. Lingkaran merah dipasangkan dengan lingkaran merah dan lingkaran biru dipasangankan dengan lingkaran biru.

Baca juga:
Yuk, Pahami Konsep Turunan Fungsi Aljabar!

Jadi, a

₁₁

akan dikalikan dengan b

₁₁

, a

₁₂

dikalikan dengan b

₂₁

, a

₂₁

dikalikan dengan b

₁₁

, dan a

₂₂

dikalikan dengan b

₂₁

.

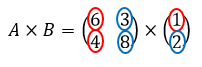
Lalu, jumlahkan hasil kali elemen-elemennya menjadi seperti ini:

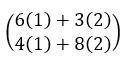
Sehingga, hasil kali matriks A dengan matriks B adalah sebagai berikut:

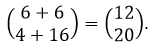
Mudah ya, teman-teman. Meskipun begitu, kamu harus banyak berlatih soal,

nih

. Kenapa? Biasanya, kamu akan masih suka bingung dan kadang suka tertukar saat mengalikan elemen matriks yang satu dengan elemen matriks yang lainnya. Jadi, jangan malas untuk sekedar latihan soal, ya!

Oke, selesai sudah materi kita kali ini, ya. Gimana? Seru

kan

belajar matriks!

Nah

, kalau kamu masih merasa latihan soal di atas tadi kurang untuk melatih kemampuan kamu, di bawah ini masih ada satu soal lagi yang bisa kamu kerjakan,

nih

. Coba kamu kerjakan dan tulis jawabanmu di kolom komentar, ya!

Baca juga:
Apa Itu Notasi Sigma?

Belajar Matematika memang

nggak

mudah,

guys

. Butuh ketekunan dan kesabaran. Kalau kamu ada materi yang masih sulit untuk dimengerti,

yuk

tanyakan langsung pertanyaanmu itu lewat
Roboguru
.
Tutor akan membantu kamu dalam membahas soal dan mengerti pelajaran

via live chat

!

Referensi:

Wirodikromo, S. dan Darmanto, M. (2019).

Matematika untuk SMA/MA Kelas XI kelompok Wajib 2

. Jakarta: Erlangga.

Artikel ini telah diperbarui pada 2 September 2022.